emre-ozer.github.io

Principal value of \(1/x\)

The following is nothing but an application of complex analysis. Nevertheless, it was something that confused me for a while when I was a student, so here's my take on it.

The expression of interest is the following:

$$ \lim _{\epsilon \rightarrow 0^{+}} \frac{1}{x \pm i \epsilon}=\mathcal{P} \frac{1}{x} \mp i \pi \delta(x). $$

To shed some light on this, let’s take a closer look. Firstly, this expression only makes sense when it is integrated over with some suitable test function \(f(x)\). Take \(f\) to be analytic over the domain of integration and consider for \(a, b > 0\) the integral

$$ \int_{(-a, b)} \frac{f(x)}{x} d x=\lim _{\epsilon \rightarrow 0^{+}} \int_{(-a, b) \backslash(-\epsilon, \epsilon)} \frac{f(x)}{x} d x+\int_{-\epsilon}^{\epsilon} \frac{f(0)}{x} d x=\mathcal{P} \int_{(-a, b)} \frac{f(x)}{x} d x+\text { divergence. } $$

Although the integral doesn’t exist, the principal value integral does as defined above. To avoid the simple pole at \(x = 0\) is to take some suitable analytic continuation of \(f(x)\) in some nice enough domain of the complex plane which includes \((−a,b)\). We can shift the pole into the imaginary axis through \(1/(x \pm i\epsilon)\) in the limit \(\epsilon \to 0\). Alternatively, we can skip over the pole by some contour that goes over or under the pole. The key point is that these two methods are equivalent.

Wlog consider the shift\(1/(x + i\epsilon)\) and a contour \(\gamma_0\) skipping over the pole:

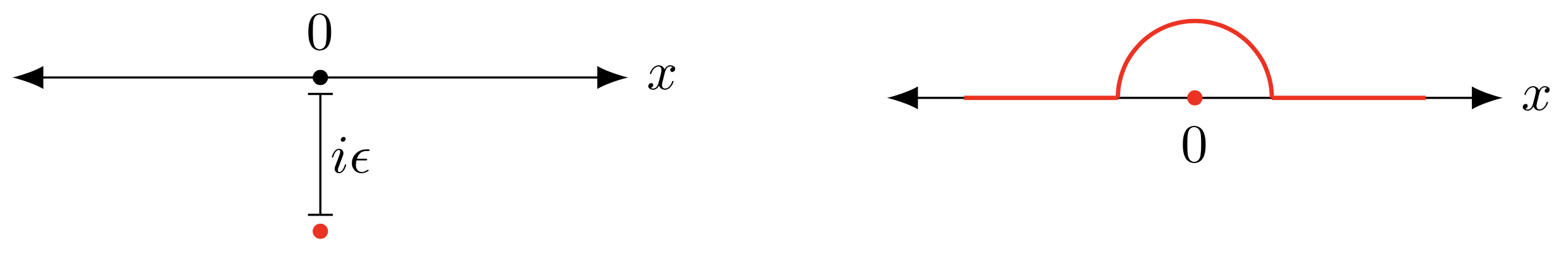
Figure showing the shifted pole and the contour.

The way to see that these two integrals are equal is to close these contours either from above by some contours \(\gamma_+ \) or from below by some contour \(\gamma_- \) such that \( f \) can be analytically continued within the closed region. If the contour \( \gamma_0 \) is closed from above, the result is

$$ \oint \frac{f(z)}{z} d z=\int_{\gamma_{+}} \frac{f(z)}{z} d z+\int_{\gamma_{0}} \frac{f(z)}{z} d z=2 \pi i \sum_{k} \operatorname{Res}\left(\frac{f(z)}{z} ; z_{k}\right). $$

The key point here is that the only pole along the real axis is at \(z = 0\). This means we don’t calculate its residue as neither integral encloses it. Clearly along \(\gamma_+\), the \(i\epsilon\) shift doesn’t matter and both integrals are equal. The same argument is applied if the contour is closed below by some \(\gamma_-\), the only difference is that the residue at \(z = 0\) or \(z = −i\epsilon\) is included. Both residues evaluate to \(f(0)\), so we’re in luck.

Now that we know both integrals are equal, we write

$$ \lim _{\epsilon \rightarrow 0^{+}} \int_{-a}^{b} \frac{f(x)}{x+i \epsilon} d x=\int_{\gamma_{0}} \frac{f(z)}{z} d z=\lim _{\epsilon \rightarrow 0^{+}} \int_{(-a, b) \backslash(-\epsilon, \epsilon)} \frac{f(x)}{x} d x+\int_{\gamma_{\epsilon}} \frac{f(z)}{z} d z, $$

where \( \gamma_\epsilon \) is the semicircle skipping over the pole. Evaluate the \(\gamma_\epsilon\) integral:

$$ \int_{\gamma_{\epsilon}} \frac{f(z)}{z} d z=\int_{\pi}^{0} i d \varphi(f(0)+\mathcal{O}(\epsilon))=-i \pi f(0)+\mathcal{O}(\epsilon). $$

Hence, we have

$$ \lim _{\epsilon \rightarrow 0^{+}} \int_{-a}^{b} \frac{f(x)}{x+i \epsilon} d x=\mathcal{P} \int_{-a}^{b} \frac{f(x)}{x} d x-i \pi f(0)=\int_{-a}^{b}\left(\mathcal{P} \frac{1}{x}-i \pi \delta(x)\right) f(x) d x. $$

This is the sense in which the very first expression is to be viewed. I’m sure I didn’t need to restrict \(f(x)\) as much as I did in this “proof”.